2.3.3. Matrices
Just as scalars are 0th-order tensors and vectors are 1st-order tensors, matrices are 2nd-order tensors. We denote matrices by bold capital letters (e.g.,𝐗, 𝐘, and 𝒁), and represent them in code by tensors with two axes. The expression 𝐀 ∈ ℝᵐˣⁿ indicates that a matrix 𝐀 contains 𝒎 × 𝒏 real-valued scalars, arranged as 𝒎 rows and 𝒏 columns. When 𝒎=𝒏, we say that a matrix is square. Visually, we can illustrate any matrix as a table. To refer to an individual element, we subscript both the row and column indices, e.g., 𝒂ᵢj is the value that belongs to 𝐀’s 𝓲ᵗʰ row and 𝒋ᵗʰ column:

In code, we represent a matrix 𝐀 ∈ ℝᵐˣⁿ by a 2nd-order tensor with shape (𝒎 , 𝒏). We can convert any appropriately sized 𝒎 × 𝒏 tensor into an 𝒎 × 𝒏 matrix by passing the desired shape to reshape:

Sometimes we want to flip the axes. When we exchange a matrix’s rows and columns, the result is called its transpose. Formally, we signify a matrix 𝐀’s transpose by 𝐀ᵀ and if 𝐁= 𝐀ᵀ, then 𝒃ᵢ𝘫=𝒂ᵢ𝘫 for all 𝓲 and 𝒋. Thus, the transpose of an 𝒎 × 𝒏 matrix is an 𝒏 × 𝒎 matrix:

In code, we can access any matrix’s transpose as follows:

Symmetric matrices are the subset of square matrices that are equal to their own transposes: 𝐀=𝐀ᵀ. The following matrix is symmetric

Matrices are useful for representing datasets. Typically, rows correspond to individual records and columns correspond to distinct attributes.
2.3.4. Tensors
While you can go far in your machine learning journey with only scalars, vectors, and matrices, eventually you may need to work with higher-order tensors. Tensors give us a generic way of describing extensions to 𝒏ᵗʰ-order arrays. We call software objects of the tensor class “tensors” precisely because they too can have arbitrary numbers of axes. While it may be confusing to use the word tensor for both the mathematical object and its realization in code, our meaning should usually be clear from context. We denote general tensors by capital letters with a special font face (e.g., 𝐗, 𝐘, and 𝒁) and their indexing mechanism (e.g., 𝒙ᵢ𝘫ᵏ and [X]₁,₂ᵢ−₁,₃) follows naturally from that of matrices.
Tensors will become more important when we start working with images. Each image arrives as a 3rd-order tensor with axes corresponding to the height, width, and channel. At each spatial location, the intensities of each color (red, green, and blue) are stacked along the channel. Furthermore, a collection of images is represented in code by a 4th-order tensor, where distinct images are indexed along the first axis. Higher-order tensors are constructed, as were vectors and matrices, by growing the number of shape components.

2.3.5. Basic Properties of Tensor Arithmetics
Scalars, vectors, matrices, and higher-order tensors all have some handy properties. For example, elementwise operations produce outputs that have the same shape as their operands.

The elementwise product of two matrices is called their Hadamard product (denoted ⊙). We can spell out the entries of the Hadamard product of two matrices 𝐀,𝐁 ∈ ℝᵐˣⁿ :
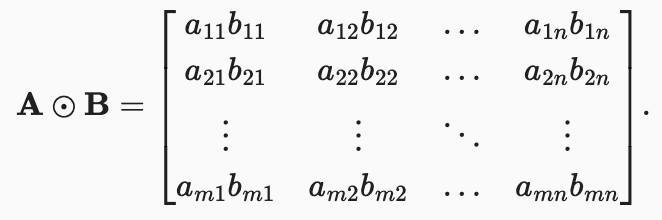
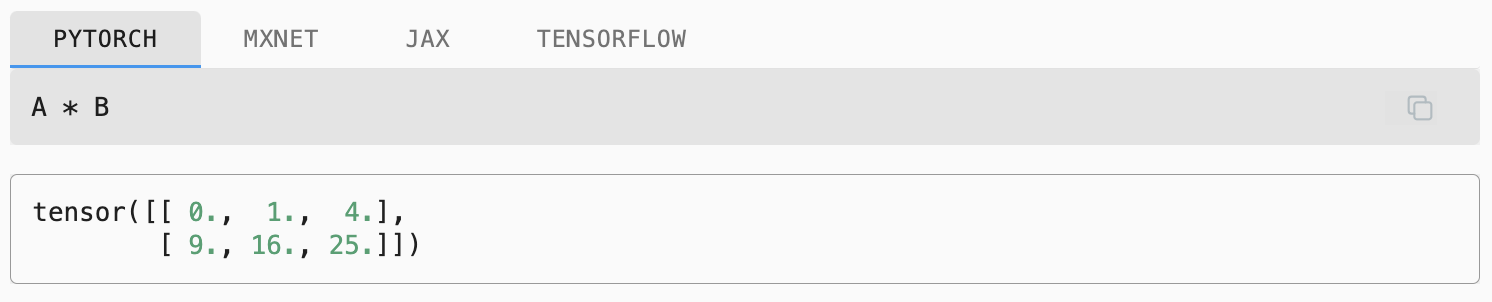
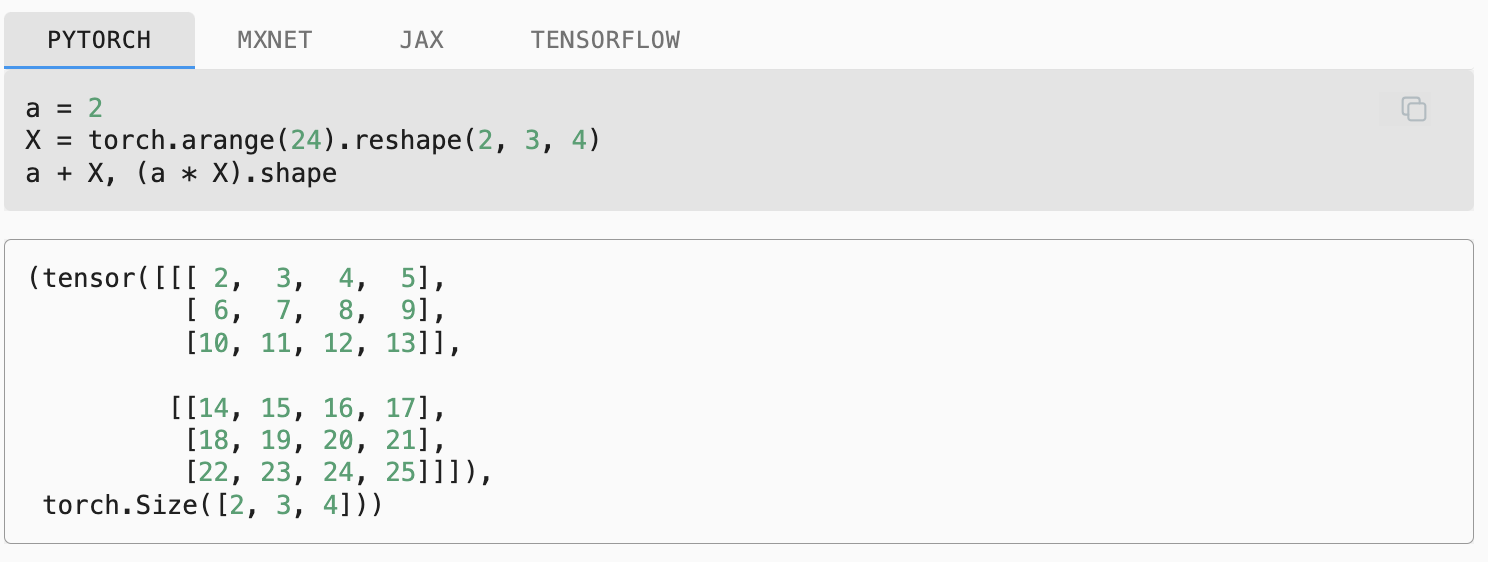
Adding or multiplying a scalar and a tensor produces a result with the same shape as the original tensor. Here, each element of the tensor is added to (or multiplied by) the scalar.
'Deep Learning' 카테고리의 다른 글
| [DIVE INTO DEEP LEARNING] 5.5. Generalization in Deep Learning (0) | 2023.12.29 |
|---|---|
| [DIVE INTO DEEP LEARNING] 2.3 Linear Algebra_scalars, vectors (1) | 2023.12.20 |
| [DIVE INTO DEEP LEARNING] 4.1 Softmax Regression (0) | 2023.12.20 |
| [DL] Transformer (0) | 2023.03.03 |
| [DL] 감성분석 (0) | 2023.02.21 |

