[DIVE INTO DEEP LEARNING] 2.3 Linear Algebra_scalars, vectors

2.3.1 Scalars

Most everyday mathematics consists of manipulating numbers one at a time. Formally, we call these values scalars. For example, the temperature in Palo Alto is a balmy 72 degrees Fahrenheit. If you wanted to convert the temperature to Celsius you would evaluate the expression 𝒄 =5/9(𝒇−32), setting 𝒇 to 72. In this equation, the values 5,9, and 32 are constant scalars. The variables 𝒄  and 𝒇 in general represent unknown scalars.

 

We denote scalars by ordinary lower-cased letters (e.g., 𝒙, 𝐲, and 𝔃) and the space of all (continuous) real-valued scalars by ℝ. For expedience, we will skip past rigorous definitions of spaces: just remember that the expression 𝒙 ∈ ℝ is a formal way to say that 𝒙 is a real-valued scalar. The symbol ∈ (pronounced “in”) denotes membership in a set. For example, 𝒙,𝐲∈{0,1} indicates that 𝒙 and 𝐲 are variables that can only take values 0 or 1.

 

Scalars are implemented as tensors that contain only one element.

(딥러닝에서는 스칼라를 하나의 값으로 표현하는데, 이 값은 0차원 텐서로도 간주된다.(모든 스칼라는 0차원 텐서이다.) 간단한 예를 들면, 파이토치에서 스칼라는 torch.tensor(3.14)와 같이 표현될 수 있는데, 이는 크기가 1이고 값이 3.14인 텐서이다.)

 

 

2.3.2 Vectors

For current purposes, you can think of a vector as a fixed-length array of scalars. As with their code counterparts, we call these scalars the elements of the vector (synonyms include entries and components). When vectors represent examples from real-world datasets, their values hold some real-world significance. For example, if we were training a model to predict the risk of a loan defaulting, we might associate each applicant with a vector whose components correspond to quantities like their income, length of employment, or number of previous defaults. If we were studying the risk of heart attack, each vector might represent a patient and its components might correspond to their most recent vital signs, cholesterol levels, minutes of exercise per day, etc. We denote vectors by bold lowercase letters, (e.g., 𝒙, 𝐲, and 𝔃).

 

Vectors are implemented as 1st-order tensors. In general, such tensors can have arbitrary lengths, subject to memory limitations. Caution: in Python, as in most programming languages, vector indices start at 0, also known as zero-based indexing, whereas in linear algebra subscripts begin at 1 (one-based indexing).

 

 

We can refer to an element of a vector by using a subscript. For example, 𝒙₂ denotes the second element of 𝐗. Since 𝒙₂ is a scalar, we do not bold it. By default, we visualize vectors by stacking their elements vertically.

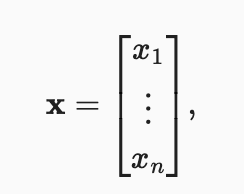
Here 𝒙₁,…,𝒙n are elements of the vector. Later on, we will distinguish between such column vectors and row vectors whose elements are stacked horizontally. Recall that we access a tensor’s elements via indexing.

 

 

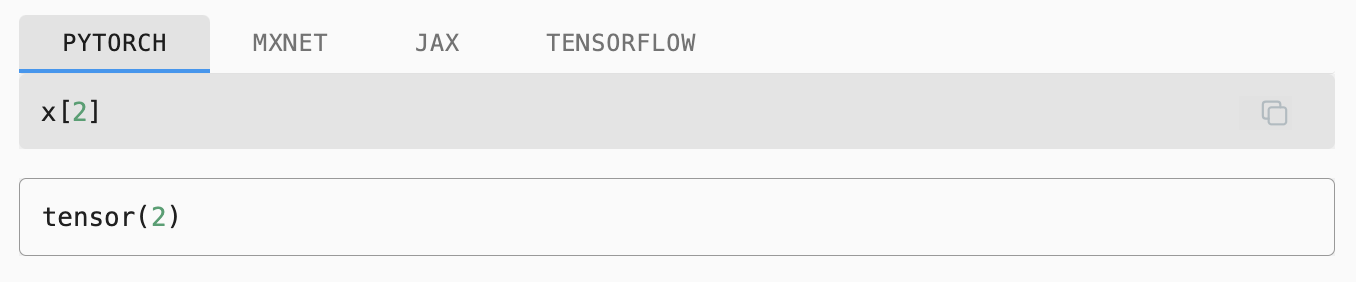
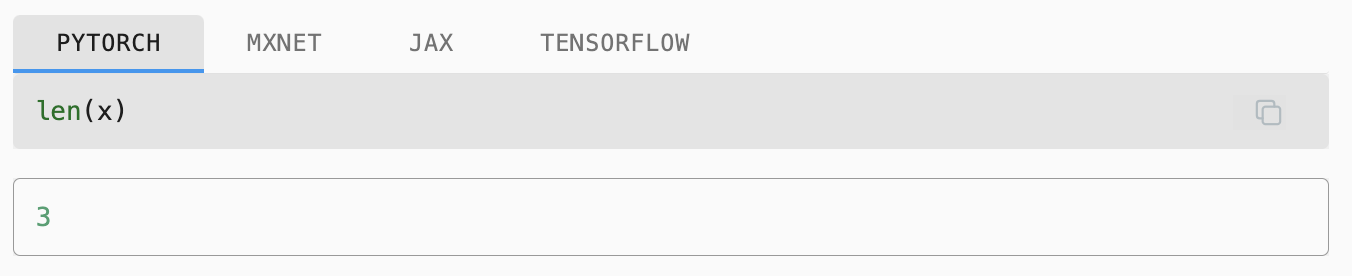
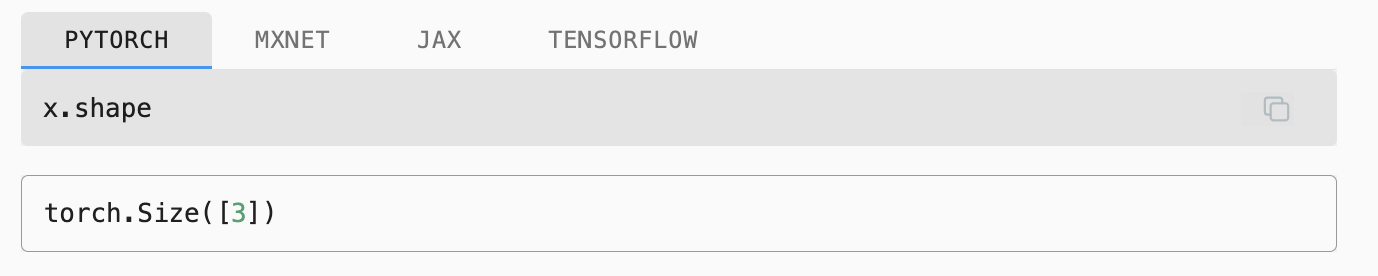
To indicate that a vector contains 𝒏 elements, we write 𝐗 ∈ ℝⁿ. Formally, we call 𝒏 the dimensionality of the vector. In code, this corresponds to the tensor’s length, accessible via Python’s built-in len function.

 

 

We can also access the length via the shape attribute. The shape is a tuple that indicates a tensor’s length along each axis. Tensors with just one axis have shapes with just one element.

 

 

 

Oftentimes, the word “dimension” gets overloaded to mean both the number of axes and the length along a particular axis. To avoid this confusion, we use order to refer to the number of axes and dimensionality exclusively to refer to the number of components. (order : 텐서의 축 수, 즉, 차원의 수. 1차원 텐서는 order 1 / dimensionality : 텐서의 각 축에 따른 구성 요소의 수. 예를 들어 2차원 텐서에서 첫번째 축의 길이와 두번째 축의 길이가 각각 3과 4라면, 이 텐서의 차원성은 (3,4))