목차
- 순방향
- XOR
- 역전파 ( Loss 함수 )
STEP01 순방향
: 아래의 코드는, 순방향이 어느 것인지 이해를 돕기위한 단순 프로세스이다. 가중치를 랜덤하게 잡을 일은 없다.
# numpy에는 sigmoid없으니 직접 함수로 만들어준다.
def sigmoid(x):
return 1.0 / (1.0 + np.exp(-x))
# 가중치를 랜덤하게 선택하자. (원래는 학습이 완료된 가중치를 사용해야 한다.)
# 원래는 양수의 값만 나와서, 2를 곱하고 -1을 해서 음수 값도 만들어준다.
# (1,3)은 1,3의 크기를 가지게 하는 것. X하나만 보면 3개의 값이 있어서
W = 2*np.random.random((1,3)) -1
# 추론
# X의 첫번째 줄과 W를 곱한 값. 마지막만 1이니 W의 마지막 * 1
np.matmul(W, X[0]) # metrics 곱
# 추론 결과
N = 4
for k in range(N):
x = X[k, :].T
v = np.matmul(W,x)
y = sigmoid(v)
print(v)
# 풀이 : X의 각 행과 W가 곱해지고 더해져서 출력된 값.
# 4개의 데이터가 각각 가중치와 곱해져서 어떤 값을 가지고 나왔는지 순방향으로 계산한 것.
# 가중치가 이제 정답을 맞추도록 학습을 시킨다.
# 지도학습 ( 정답을 알려준다.)
X = np.array([
[0, 0, 1],
[0, 1, 1],
[1, 0, 1],
[1, 1, 1]
])
D = np.array([
[0], [0], [1], [1]
])# 순방향 연산
def calc_output(W, x):
v = np.matmul(W, x)
y = sigmoid(v)
return y
# 오차 계산하는 함수 y가 추론값, d가 정답
def calc_error(d, y):
e = d - y # 오차
delta = y * (1-y) * e # y*(1-y)는 시그모이드. delta는 시그모이드의 미분값
return delta
# 한 epoch에 수행되는 W의 계산. GradientDesent 모든 데이터에 대한 epoch 돈다. 가중치 W return
def delta_GD(W, X, D, alpha):
for k in range(4):
x = X[k, :].T
d = D[k]
y = calc_output(W, x) # 순방향 연산 결과
delta = calc_error(d, y)
dW = alpha*delta*x # 가중치가 변화해야 하는 양
W = W + dW
return W
# 돌려보자
W = 2*np.random.random((1,3)) -1
alpha = 0.9
for epoch in range(10000):
W = delta_GD(W, X, D, alpha)
print(W)
N = 4
for k in range(N):
x = X[k,:].T
v = np.matmul(W, x)
y = sigmoid(v)
print(y)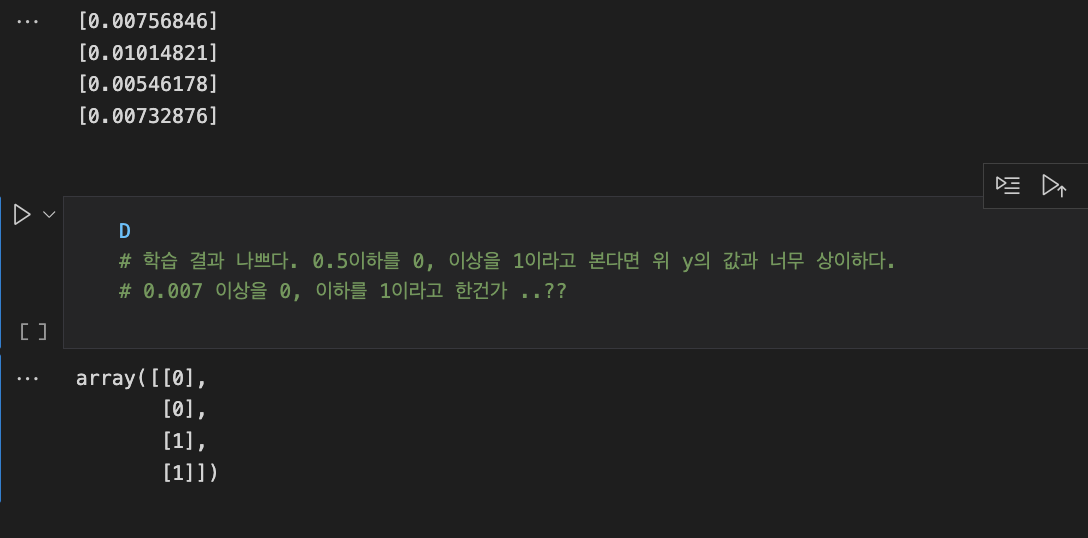
위의 코드 출력문이다. D는 0, 0, 1,1의 값을 갖고 있었는데, 0과 1을 나눌 수 있는 기준이 보이지 않는다.
STEP02 XOR
# [0, 1]이나 [1,0]일때만 [1]의 값을 갖게 한다.
X = np.array([
[0, 0, 1],
[0, 1, 1],
[1, 0, 1],
[1, 1, 1]
])
D = np.array([
[0], [1], [1], [0]
])
W = 2*np.random.random((1,3)) -1
alpha = 0.9
for epoch in range(10000):
W = delta_GD(W, X, D, alpha)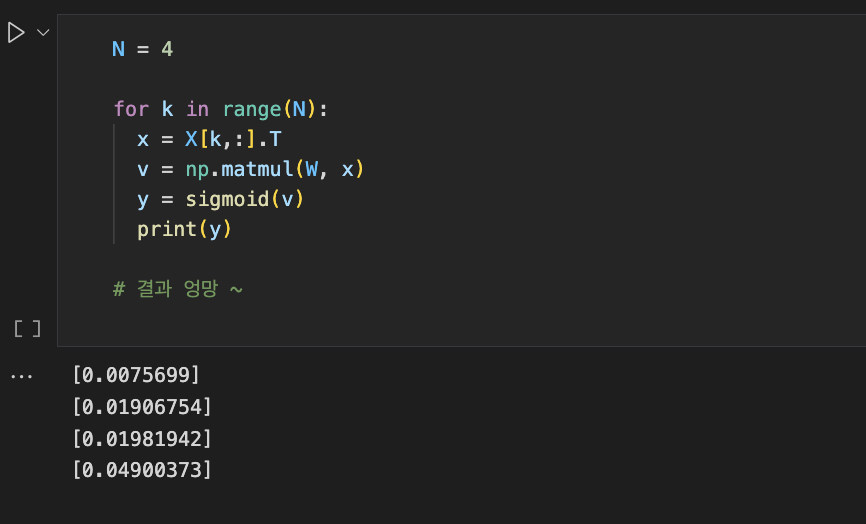
이 또한 결과가 엉망임을 확인 가능하다.
STEP03 역전파
XOR 극복하기
- 다층의 경우, 1차 2차 은닉층의 오차를 계산할 수 없다. (정답을 모르기에 은닉층의 가중치를 계산할 수 없기 때문에)
- 이를 해결하기 위한 역전파 개념이 등장했다.
- 출력층에서 델타를 만들어서 그 전 은닉층으로 보낸다.
프로세스
- 출력층의 delta를 계산해서 은닉층으로 보낸 뒤, 그걸 가지고 은닉층의 error1을 계산하고, 그게 시그모이드의 미분차와 곱해져서 또 다른 delta를 만들어낸다. (=오차의 역전파)
# output 함수
def calc_output(W1, W2, x):
v1 = np.matmul(W1, x) # 첫번째 레이어와 가중치 곱
y1 = sigmoid(v1)
v = np.matmul(W2, y1)
y = sigmoid(v)
return y, y1
# 출력층의 델타 계산
def calc_delta(d, y):
e = d-y
delta = y * (1-y) * e
return delta
# 은닉층의 델타 계산
def calc_delta1(W2, delta, y1):
e1 = np.matmul(W2.T, delta)
delta1 = y1*(1-y1) * e1
return delta1
# 역전파 코드
def backprop_XOR(W1, W2, X, D, alpha):
for k in range(4):
x = X[k, :].T
d = D[k]
y, y1 = calc_output(W1, W2, x)
delta = calc_delta(d, y)
delta1 = calc_delta1(W2, delta, y1)
dW1 = (alpha * delta1).reshape(4, 1) * x.reshape(1,3)
W1 = W1 + dW1
dW2 = alpha * delta * y1
W2 = W2 + dW2
return W1, W2
#
X = np.array([[0, 0, 1],
[0, 1, 1],
[1, 0, 1],
[1, 1, 1]])
D = np.array([[0], [1], [1], [0]])
W1 = 2*np.random.random((4,3)) -1 # 크기가 왜 4,3이냐면, 우리가 만드는게 첫번째에서 3개를 받고, 2번째 층에서 4개, 결론 1개.
W2 = 2*np.random.random((1,4)) -1
# 학습
alpha = 0.9
for epoch in range(10000):
W1, W2 = backprop_XOR(W1, W2, X ,D, alpha)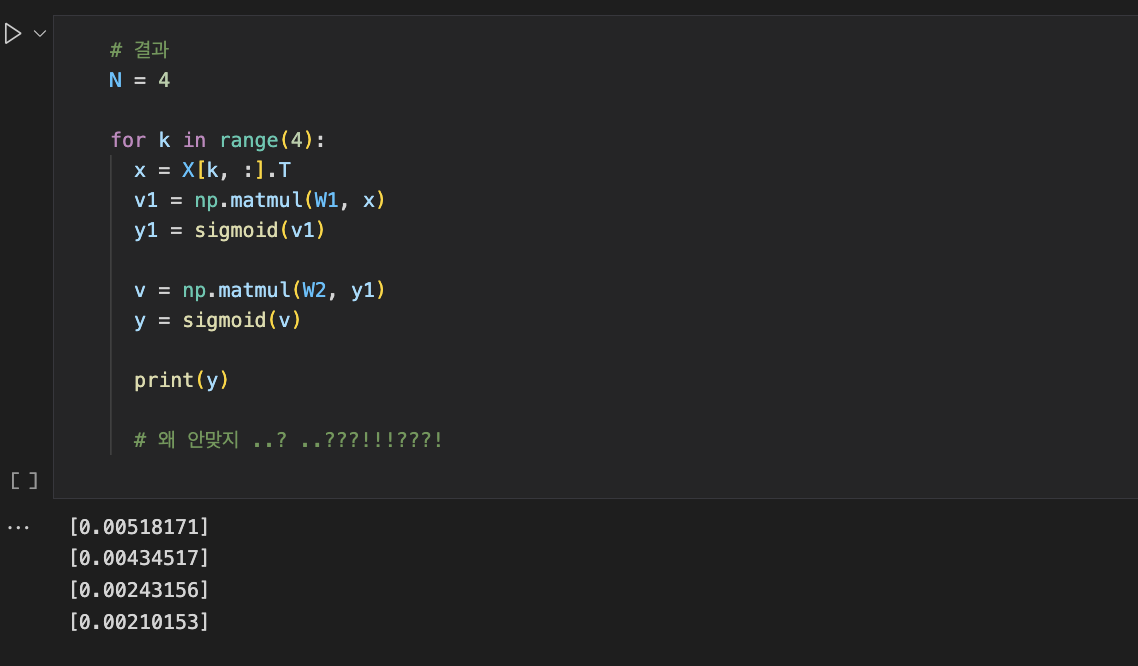
이정도로 코드를 수정해도 정답과 맞지 않았다.
그래서 Loss함수로 교체하여 다시 돌려보았다. (cross entropy와 미분하면 델타와 같다. 즉, 오차를 말한다.)
# Loss 함수 교체
# cross entropy는 미분하면 델타와 같다. 즉, 오차
def calcDelta_ce(d, y):
e = d - y
delta = e
return e
# 은닉층
def calcDelta1_ce(W2, delta, y1):
e1 = np.matmul(W2.T, delta)
delta1 = y1*(1-y1)*e1
return delta1
def BackpropCE(W1, W2, X, D, alpha):
for k in range(4):
x = X[k, :].T
d = D[k]
y, y1 = calc_output(W1, W2, x)
delta = calcDelta_ce(d, y)
delta1 = calcDelta1_ce(W2, delta, y1)
dW1 = (alpha*delta1).reshape(4, 1) * x.reshape(1,3)
W1 = W1 + dW1
dW2 = alpha * delta * y1
W2 = W2 + dW2
return W1, W2
W1 = 2*np.random.random((4, 3)) -1
W2 = 2*np.random.random((1, 4)) -1
alpha = 0.9
for epoch in range(10000):
W1, W2 = BackpropCE(W1, W2, X, D, alpha)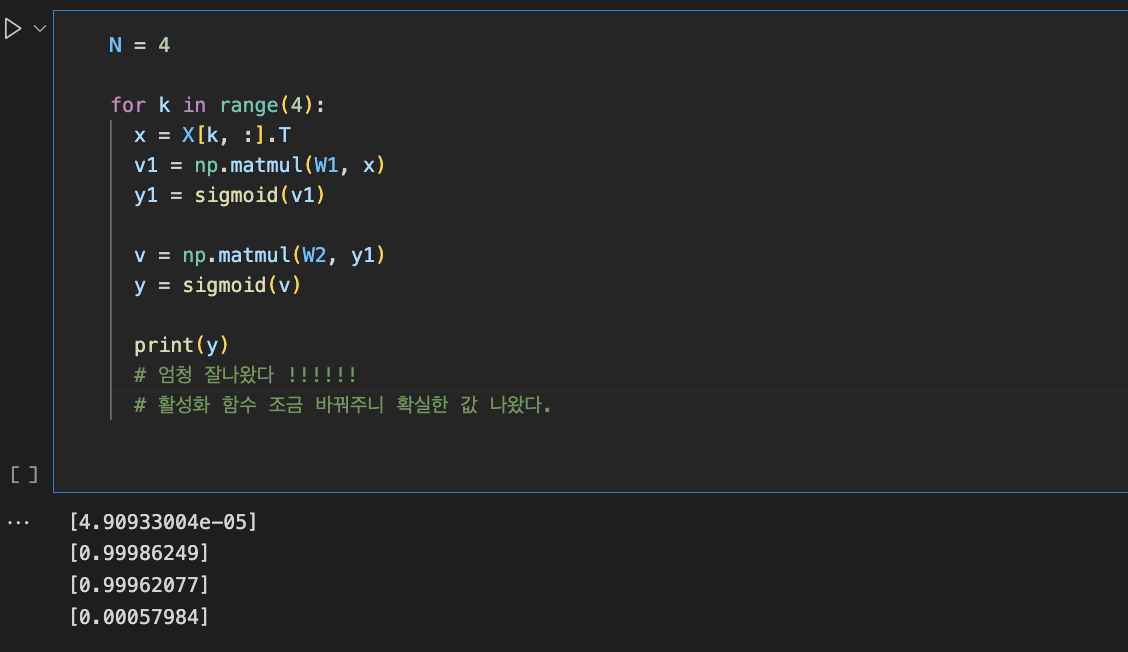
드디어 정답이 출력되었다. (0, 1, 1, 0)
'Deep Learning' 카테고리의 다른 글
| [DL] t-SNE (0) | 2023.02.19 |
|---|---|
| [DL] AutoEncoder. Latent Vector (0) | 2023.02.19 |
| [DL] Transfer learning _ 기본 option (0) | 2023.02.16 |
| [DL] options in DeepLearning ( Transfer learning) (0) | 2023.02.16 |
| [DL] CNN (0) | 2023.02.08 |



